Combined City Population: Measles Outbreak Modeling
combined_cities.Rmd
library(multigroup.vaccine)
library(socialmixr)
library(ggplot2)
# Load city data files
hildale_path <- system.file("extdata", "hildale_ut_2023.csv", package = "multigroup.vaccine")
colorado_city_path <- system.file("extdata", "colorado_city_az_2023.csv", package = "multigroup.vaccine")Measles Model Setup
For measles outbreak modeling in the combined population of Hildale, UT and Colorado City, AZ, we’ll use granular age groups that separate school levels: pre-school (0-4), elementary (5-12), middle school (13-14), high school (15-18), and adult age bands.
# Age groups: 0-4, 5-11 (elementary K-6), 12-13 (middle 7-8), 14-17 (high 9-12), 18-24, 25-34, 35-44, 45-54, 55-64, 65+
agelims <- c(0, 5, 12, 14, 18, 25, 35, 45, 55, 65)
# Vaccine effectiveness by age group
ageveff <- rep(0.97, length(agelims)) # All groups have high effectiveness
ageveff[1] <- 0.93 # Under 5 may have slightly lower effectiveness
# Initial infection in the 25-29 age group (working age adults)
# This corresponds to age group 25-34 (index 6)
initgrp <- 6Getting Combined City Population Data
We’ll combine the populations of Hildale, UT and Colorado City, AZ by disaggregating their ACS 5-year age groups into single-year ages, then summing across both cities, and finally aggregating into school age groups.
# Get single-year age data for both cities
cities <- c("Hildale city, Utah", "Colorado City town, Arizona")
city_paths <- c(hildale_path, colorado_city_path)
single_year_data <- list()
for (i in seq_along(cities)) {
data <- getCityData(
city_name = cities[i],
csv_path = city_paths[i],
age_groups = NULL # Single-year ages
)
single_year_data[[cities[i]]] <- data
}
# Combine populations by summing across cities for each age
combined_ages <- single_year_data[[1]]$age_pops * 0 # Initialize with zeros
age_labels <- single_year_data[[1]]$age_labels
total_pop <- 0
for (city_data in single_year_data) {
combined_ages <- combined_ages + city_data$age_pops
total_pop <- total_pop + city_data$total_pop
}
# Now aggregate into school age groups
ages_numeric <- 0:85 # Ages 0 through 85
grouped <- aggregateByAgeGroups(ages_numeric, combined_ages, agelims)
#> Aggregating ages 0 to 4: sum = 182
#> Aggregating ages 5 to 11: sum = 569.4
#> Aggregating ages 12 to 13: sum = 246.4
#> Aggregating ages 14 to 17: sum = 504.2
#> Aggregating ages 18 to 24: sum = 677
#> Aggregating ages 25 to 34: sum = 543
#> Aggregating ages 35 to 44: sum = 341
#> Aggregating ages 45 to 54: sum = 468
#> Aggregating ages 55 to 64: sum = 263
combined_data <- list(
city = "Combined Hildale, UT and Colorado City, AZ",
year = 2023,
total_pop = total_pop,
age_pops = grouped$pops,
age_labels = grouped$labels,
data = NULL # No single data frame for combined
)
cat("Combined Population Data:\n")
#> Combined Population Data:
cat("Total population:", format(combined_data$total_pop, big.mark = ","), "\n")
#> Total population: 3,899
cat("Age distribution:\n")
#> Age distribution:
for (i in seq_along(combined_data$age_labels)) {
pct <- 100 * combined_data$age_pops[i] / combined_data$total_pop
cat(sprintf(" %s: %s (%.1f%%)\n",
combined_data$age_labels[i],
format(combined_data$age_pops[i], big.mark = ","),
pct))
}
#> 0to4: 182 (4.7%)
#> 5to11: 569.4 (14.6%)
#> 12to13: 246.4 (6.3%)
#> 14to17: 504.2 (12.9%)
#> 18to24: 677 (17.4%)
#> 25to34: 543 (13.9%)
#> 35to44: 341 (8.7%)
#> 45to54: 468 (12.0%)
#> 55to64: 263 (6.7%)
#> 65plus: 105 (2.7%)Scenario 1: Current Vaccination Coverage (95% adult rate)
Let’s model outbreaks under estimated vaccination coverage levels for the combined community.
# Vaccination coverage rates
# Assume 95% coverage for adults (19+), lower for children
vaxcov <- c(
0.44, # under 5
0.45, # 5-11 elementary
0.50, # 12-13 middle
0.45, # 14-17 high
0.95, # 18-24
0.95, # 25-34
0.95, # 35-44
0.95, # 45-54
0.95, # 55-64
0.95 # 65+
)
current_coverage_95 <- vaxcov # For compatibility with interpolation code
# Run the measles model using getOutputTable
results1 <- getOutputTable(
agelims = agelims,
agepops = combined_data$age_pops,
agecovr = vaxcov,
ageveff = ageveff,
initgrp = initgrp
)
cat("Combined Cities - Current Vaccination Coverage\n")
#> Combined Cities - Current Vaccination Coverage
print(as.data.frame(results1), row.names = FALSE)
#> R0 R0local Rv pEscape escapeInfTot under5 5to11 12to13 14to17 18to24
#> 10 20.61422 10.82586 0.640 988 97 320 126 284 49
#> 11 22.67564 11.90844 0.646 996 99 320 126 284 50
#> 12 24.73706 12.99103 0.681 1001 101 320 126 284 51
#> 13 26.79848 14.07361 0.682 1006 103 320 126 284 51
#> 14 28.85990 15.15620 0.743 1010 104 320 126 284 52
#> 15 30.92132 16.23879 0.715 1013 105 320 126 284 52
#> 16 32.98274 17.32137 0.741 1015 106 320 126 284 52
#> 17 35.04417 18.40396 0.749 1017 106 320 126 284 52
#> 18 37.10559 19.48654 0.764 1019 107 320 126 284 53
#> 25to34 35to44 45to54 55to64 65+
#> 37 25 31 14 4
#> 38 25 32 15 4
#> 39 26 33 16 4
#> 40 26 34 16 5
#> 41 26 35 17 5
#> 41 26 35 17 5
#> 42 27 35 18 5
#> 42 27 36 18 5
#> 42 27 36 18 6
# Extract results for R0=15 (typical measles R0)
r0_15_idx <- which(results1[, "R0"] == 15)
final_size1 <- results1[r0_15_idx, "escapeInfTot"]
percent_infected1 <- 100 * final_size1 / combined_data$total_pop
cat("Final outbreak size (R0=15):", format(final_size1, big.mark = ","), "\n")
#> Final outbreak size (R0=15): 1,013
cat("Overall % infected:", sprintf("%.2f%%", percent_infected1), "\n")
#> Overall % infected: 25.98%Scenario 2: Linear Interpolation of Adult Vaccination Rates
Now let’s examine the impact using linear interpolation of adult vaccination rates (similar to the individual city analysis).
# Linear interpolation of adult vaccination rates
# Interpolate between 45% (end of high school) and 95% (older adults)
adult_ages <- c(15, 20, 25, 30, 35, 40, 45, 50)
adult_rates <- seq(0.45, 0.95, length.out = length(adult_ages))
vaxcov2 <- current_coverage_95 # Start with current coverage
for (i in seq_along(adult_ages)) {
age <- adult_ages[i]
rate <- adult_rates[i]
age_idx <- which(agelims[-length(agelims)] == age)
if (length(age_idx) > 0) {
vaxcov2[age_idx] <- rate
}
}
cat("Scenario 2: Linear interpolated adult vaccination coverage\n")
#> Scenario 2: Linear interpolated adult vaccination coverage
cat("Vaccination coverage rates:", paste0(100 * vaxcov2, "%", collapse = ", "), "\n")
#> Vaccination coverage rates: 44%, 45%, 50%, 45%, 95%, 59.2857142857143%, 73.5714285714286%, 87.8571428571429%, 95%, 95%
results2 <- getOutputTable(
agelims = agelims,
agepops = combined_data$age_pops,
agecovr = vaxcov2,
ageveff = ageveff,
initgrp = initgrp
)
cat("Combined Cities - Linear Interpolated Adult Vaccination Coverage\n")
#> Combined Cities - Linear Interpolated Adult Vaccination Coverage
print(as.data.frame(results2), row.names = FALSE)
#> R0 R0local Rv pEscape escapeInfTot under5 5to11 12to13 14to17 18to24
#> 10 20.61422 10.88977 0.720 1289 102 320 126 284 51
#> 11 22.67564 11.97875 0.756 1297 104 320 126 284 52
#> 12 24.73706 13.06773 0.784 1302 105 320 126 284 52
#> 13 26.79848 14.15671 0.791 1306 106 320 126 284 52
#> 14 28.85990 15.24568 0.803 1309 106 320 126 284 53
#> 15 30.92132 16.33466 0.820 1311 107 320 126 284 53
#> 16 32.98274 17.42364 0.850 1313 107 320 126 284 53
#> 17 35.04417 18.51262 0.832 1314 107 320 126 284 53
#> 18 37.10559 19.60159 0.854 1315 108 320 126 284 53
#> 25to34 35to44 45to54 55to64 65+
#> 223 95 65 17 5
#> 225 96 66 18 5
#> 227 97 67 18 5
#> 228 97 67 19 6
#> 229 97 68 19 6
#> 230 98 68 19 6
#> 230 98 68 20 6
#> 230 98 68 20 6
#> 231 98 69 20 7
final_size2 <- results2[r0_15_idx, "escapeInfTot"]
percent_infected2 <- 100 * final_size2 / combined_data$total_pop
cat("Final outbreak size (R0=15):", format(final_size2, big.mark = ","), "\n")
#> Final outbreak size (R0=15): 1,311
cat("Overall % infected:", sprintf("%.2f%%", percent_infected2), "\n")
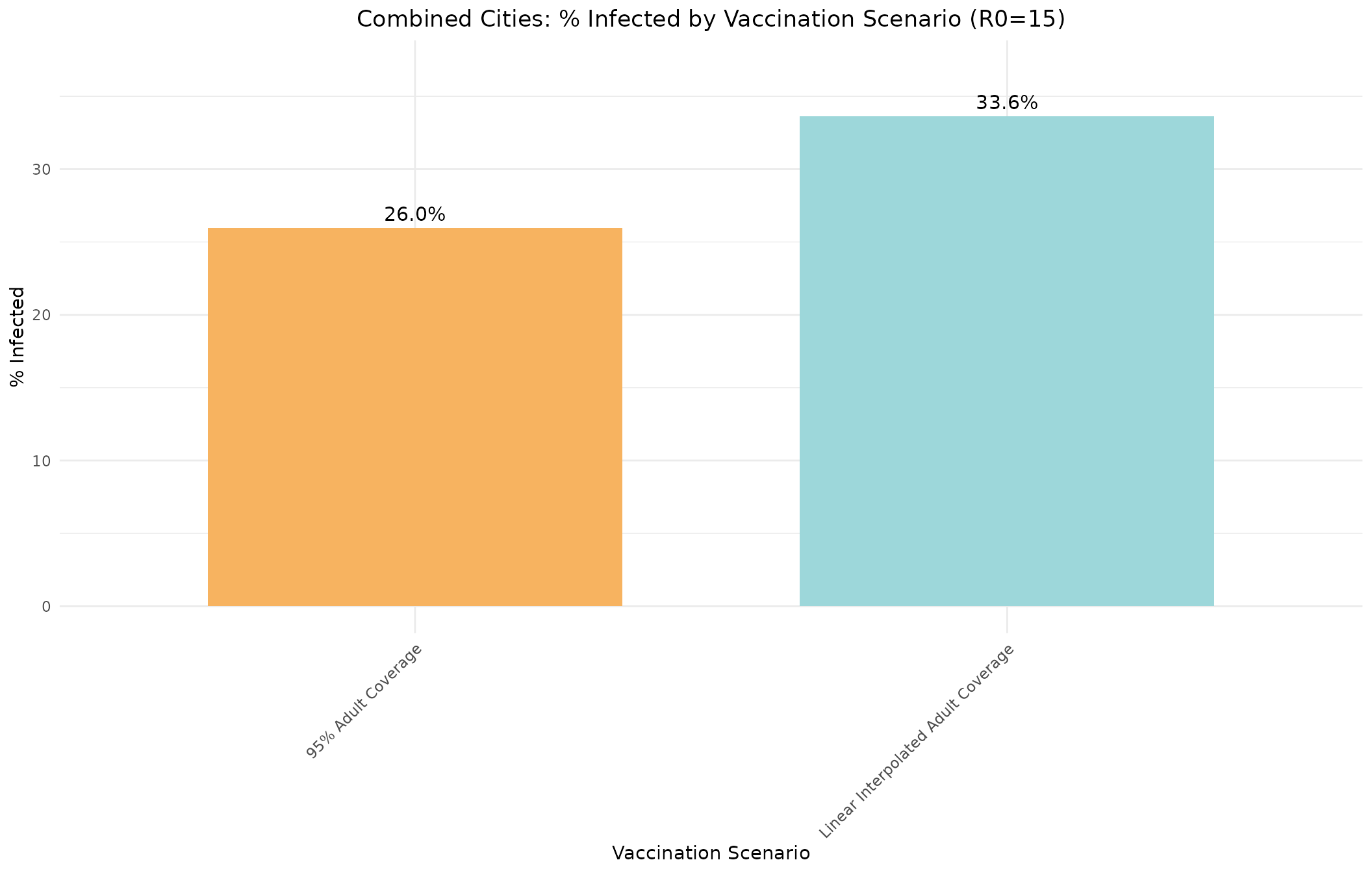
#> Overall % infected: 33.62%Scenario Comparison
Let’s compare the two scenarios side by side.
# Create data frame for ggplot
comparison_data <- data.frame(
Scenario = factor(c("95% Adult Coverage", "Linear Interpolated Adult Coverage"),
levels = c("95% Adult Coverage", "Linear Interpolated Adult Coverage")),
Percent_Infected = c(percent_infected1, percent_infected2),
Final_Size = c(final_size1, final_size2),
Color = c("#f7b360", "#9dd7da")
)
ggplot(comparison_data, aes(x = Scenario, y = Percent_Infected, fill = Color)) +
geom_bar(stat = "identity", width = 0.7) +
geom_text(aes(label = sprintf("%.1f%%", Percent_Infected)), vjust = -0.5, size = 4) +
scale_fill_identity() +
labs(title = "Combined Cities: % Infected by Vaccination Scenario (R0=15)",
x = "Vaccination Scenario",
y = "% Infected") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1),
plot.title = element_text(hjust = 0.5)) +
ylim(0, max(comparison_data$Percent_Infected) * 1.1)